Функ ций вида y kx b. Функция прямой. Защита работы, выполненной с помощью компьютера

Удобная для того, чтобы, задав конкретное значение независимой переменной х (аргумента), вычислить соответствующее значение зависимой переменной у. Например, если дана функция у = х 2 , т.е. f(x) = х 2 , то при х = 1 получаем у = 1 2 = 1; короче это записывают так: f(1) = 1. При х = 2 получаем f(2)= 2 2 = 4, т. е. у = 4; при х = - 3 получаем f(- 3) = (- З) 2 = 9, т. е. у = 9, и т. д.

Уже в 7-м классе мы с вами начали понимать, что в равенстве у = f(х) правая часть, т.е. выражение f(x), не исчерпывается перечисленными выше четырьмя случаями (С, kx, kx + m, х 2).

Так например, нам уже встречались кусочные функции, т. е. функции , заданные разными формулами на разных промежутках. Вот одна из таких функций:у = f(x), где

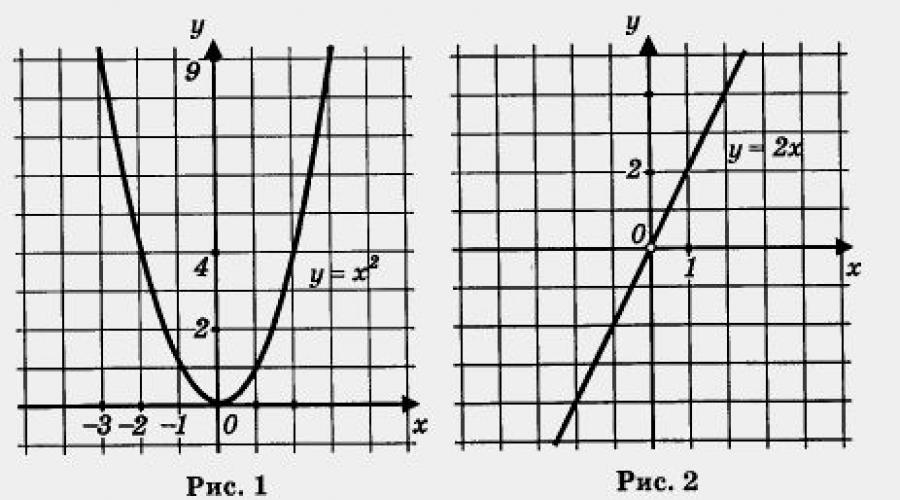
Помните, как строить графики таких функций? Сначала надо построить параболу у = х 2 и взять ее часть при х < 0 (левая ветвь параболы, рис. 1), затем надо построить прямую у = 2х и взять ее часть при х > 0 (рис. 2). И, наконец, надо обе выделенные части объединить на одном рисунке, т. е. построить на одной координатной плоскости (см. рис. 3).

Теперь наша задача состоит в следующем: пополнить запас изученных функций. В реальной жизни встречаются процессы, описываемые различными математическими моделями вида у = f(x), не только теми, что мы перечислили выше. В этом параграфе мы рассмотрим функцию у = kx 2 , где коэффициент k - любое отличное от нуля число.

На самом деле функция у = kx 2 в одном случае вам немного знакома. Смотрите: если k = 1, то получаем у = х 2 ; эту функцию вы изучили в 7-м классе и, наверное, помните, что ее графиком является парабола (рис. 1). Обсудим, что происходит при других значениях коэффициента k.

Рассмотрим две функции: у = 2х 2 и у = 0,5x 2 . Составим таблицу значений для первой функции у = 2х 2:

Построим точки (0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1,5; 4,5), (-1,5; 4,5) на координатной плоскости (рис. 4); они намечают некоторую линию, проведем ее (рис. 5).

Составим таблицу значений для второй функции у = 0,5x 2:

Построим точки (0; 0), (1; 0,5), (-1; 0,5), (2; 2), (-2; 2), C; 4,5), (-3; 4,5) на координатной плоскости (рис. 6); они намечают некоторую линию, проведем ее (рис. 7)

.

Точки, изображенные на рис. 4 и 6, называют иногда контрольными точками для графика соответствующей функции.

Сравните рисунки 1, 5 и 7. Не правда ли, проведенные линии похожи? Каждую из них называют параболой; при этом точку (0; 0) называют вершиной параболы, а ось у - осью симметрии параболы. От величины коэффициента k зависит «скорость устремления» ветвей параболы вверх или, как еще говорят, «степень крутизны» параболы. Это хорошо видно на рис. 8, где все три построенные выше параболы расположены на одной координатной плоскости.

Точно так же обстоит дело с любой другой функцией вида у = kx 2 , где k > 0. Графиком ее является парабола с вершиной в начале координат , ветви параболы направлены вверх, причем тем круче, чем больше коэффициент k. Ось у является осью симметрии параболы. Кстати, ради краткости речи математики часто вместо длинной фразы «парабола, служащая графиком функции у = kx 2 », говорят «парабола у = кх 2 », а вместо термина «ось симметрии параболы» используют термин «ось параболы».

Вы замечаете, что имеется аналогия с функцией у = kx? Если k > 0, то графиком функции у = kx является прямая, проходящая через начало координат (помните, мы говорили коротко:прямая у = kx), причем и здесь от величины коэффициента k зависит «степень крутизны» прямой. Это хорошо видно на рис. 9, где в одной системе координат изображены графики линейных функций у = kx при трех значениях коэффициента

Вернемся к функции у = kx 2 . Выясним, как обстоит дело в случае отрицательного коэффициента ft. Построим, например, график функции

у = - х 2 (здесь k = - 1). Составим таблицу значении:

Отметим точки (0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; - 9) на координатной плоскости (рис. 10); они намечают некоторую линию, проведем ее (рис. 11). Это - парабола с вершиной в точке (0; 0), ось у - ось симметрии, но в отличие от случая, когда k > 0, на этот раз ветви параболы направлены вниз. Аналогично обстоит дело и для других отрицательных значений коэффициента k.

Итак, графиком функции является парабола с вершиной в начале координат; ось у является осью параболы; ветви параболы направлены вверх приk>0 u вниз при k<0.

Отметим еще, что парабола у = kx 2 касается оси х в точке (0; 0), т. е. одна ветвь параболы плавно переходит в другую, как бы прижимаясь к оси х.

Если построить в одной системе координат графики функций у = х 2 и у = - х2, то нетрудно заметить, что эти параболы симметричны друг другу относительно оси х, что хорошо видно на рис. 12. Точно так же симметричны друг другу относительно оси х параболы у = 2х 2 и у = - 2х 2 (не поленитесь, постройте эти
две параболы в одной системе координат и убедитесь в справедливости сделанного утверждения).

Вообще, график функции у = - f(x) симметричен графику функции у = f(x) относительно оси абсцисс.

Свойства функции у = kx 2 при k > 0

Описывая свойства этой функции, мы будем опираться на ее геометрическую модель - параболу (рис. 13).

1. Так как для любого значения х по формуле у = kx 2 можно вычислить соответствующее значение у, то функция определена в любой точке х (при любом значении аргумента х). Короче это записывают так: область определения функции есть (-оо, +оо), т. е. вся координатная прямая.

2. у = 0 при х = 0; у > О при . Это видно и по графику функции (он весь расположен выше оси х), но можно обосновать и без помощи графика: если

То kx 2 > О как произведение двух положительных чисел k и х 2 .

3. у = kx 2 - непрерывная функция. Напомним, что этот термин мы рассматриваем пока как синоним предложения «график функции есть сплошная линия, которую можно начертить, не отрывая карандаша от бумаги». В старших классах будет дано более точное математическое истолкование понятия непрерывности функции, не опирающееся на геометрическую иллюстрацию.

4.y/ наим = 0 (достигается при х = 0); у наи6 не существует.

Напомним, что {/наим - это наименьшее значение функции, а Унаиб. - наибольшее значение функции на заданном промежутке; если промежуток не указан, то унаим- и у наиб, - соответственно наименьшее и наибольшее значения функции в области определения.

5. Функция у = kx 2 возрастает при х > О и убывает при х < 0.

Напомним, что в курсе алгебры 7-го класса мы договорились называть функцию, график которой на рассматриваемом промежутке идет слева направо как бы «в горку», возрастающей, а функцию , график которой на рассматриваемом промежутке идет слева направо как бы «под горку», - убывающей. Более точно можно сказать так: функцию у = f (x) называют возрастающей на промежутке X, если на этом промежутке большему значению аргумента соответствует большее значение функции; функцию у = f (x) называют убывающей на промежутке X, если на этом промежутке большему значению аргумента соответствует меньшее значение функции.

В учебнике «Алгебра-7» процесс перечисления свойств функции мы называли чтением графика. Процесс чтения графика будет у нас постепенно становиться все насыщеннее и интереснее - по мере изучения новых свойств функций. Те пять свойств, которые перечислены выше, мы обсуждали в 7-м классе для изученных там функций. Добавим одно новое свойство.

Функцию у = f(x) называют ограниченной снизу, если все значения функции больше некоторого числа. Геометрически это означает, что график функции расположен выше некоторой прямой , параллельной оси х.

А теперь посмотрите: график функции у = kx 2 расположен выше прямой у = - 1 (или у = - 2, это неважно) - она проведена на рис. 13. Значит, у - kx2 (k > 0) - ограниченная снизу функция.

Наряду с функциями, ограниченными снизу, рассматривают и функции, ограниченные сверху. Функцию у - f(x) называют ограниченной сверху, если все значения функции меньше некоторого числа. Геометрически это означает, что график функции расположен ниже некоторой прямой, параллельной оси х.
Имеется ли такая прямая для параболы у = kx 2 , где k > 0? Нет. Это значит, что функция не является ограниченной сверху.

Итак, мы получили еще одно свойство, добавим его к тем пяти, что указаны выше.

6. Функция у = kx 2 (k > 0) ограничена снизу и не ограничена сверху.

Свойства функции у = kx 2 при k < 0

При описании свойств этой функции мы опираемся на ее геометрическую модель - параболу (рис. 14).

1.Область определения функции - (-оо, +оо).

2. у = 0 при х = 0; у < 0 при .

З.у = kx 2 - непрерывная функция.
4. у наи6 = 0 (достигается при х = 0), унаим не существует.

5. Функция возрастает при х < 0, убывает при х > 0.

6.Функция ограничена сверху и не ограничена снизу.

Дадим пояснения последнему свойству: имеется прямая, параллельная оси х (например, у = 1, она проведена на рис. 14), такая, что вся парабола лежит ниже этой прямой; это значит, что функция ограничена сверху. С другой стороны, нельзя провести такую прямую, параллельную оси х, чтобы вся парабола была расположена выше этой прямой; это значит, что функция не ограничена снизу.

Использованный выше порядок ходов при перечислении свойств функции не является законом, пока он сложился хронологически именно таким.

Более-менее определенный порядок ходов мы выработаем постепенно и унифицируем в курсе алгебры 9-го класса.

Пример 1. Найти наименьшее и наибольшее значения функции у = 2х 2 на отрезке: а) ; б) [- 2, - 1]; в) [- 1, 1,5].

а) Построим график функции у = 2х 2 и выделим его часть на отрезке (рис. 15). Замечаем, что 1/наим. = 0 (достигается при х = 0), а у наиб = 8 (достигается при х = 2).

б) Построим график функции у = 2х 2 и выделим его часть на отрезке [- 2, - 1] (рис. 16). Замечаем, что 2/наим = 2 (достигается при х = - 1), а y наиб = 8 (достигается при х = - 2).

в) Построим график функции у = 2х 2 и выделим его часть на отрезке [- 1, 1,5] (рис. 17). Замечаем, что унанм = 0 (достигается при х = 0), а y наиб достигается в точке х = 1,5; подсчитаем это значение:(1,5) = 2-1,5 2 = 2- 2,25 = 4,5. Итак, y наиб =4,5.

Пример 2. Решить уравнение - х 2 = 2х - 3.

Решение. В учебнике «Алгебра-7» мы выработали алгоритм графического решения уравнений, напомним его.

Чтобы графически решить уравнение f(x) = g (x), нужно:

1) рассмотреть две функции у = -x 2 и у = 2x -3;
2) построить график функции i/ = / (х) ;
3) построить график функции у = g (x);
4) найти точки пересечения построенных графиков; абсцис-
сы этих точек - корни уравнения f(x) = g (x).

Применим этот алгоритм к заданному уравнению.
1) Рассмотрим две функции: у = - х2 и у = 2х - 3.
2) Построим параболу - график функции у = - х 2 (рис. 18).

3) Построим график функции у = 2х - 3. Это - прямая, для ее построения достаточно найти любые две точки графика. Если х = 0, то у = - 3; если х = 1,то у = -1. Итак, нашли две точки (0; -3) и (1; -1). Прямая, проходящая через эти две точки (график функции у = 2х - 3), изображена на том же чертеже (см. рис. 18).

4) По чертежу находим, что прямая и парабола пересекаются в двух точках А(1; -1) и Б(-3; -9). Значит, данное уравнение имеет два корня: 1 и - 3 - это абсциссы точек А и В.

Ответ: 1,-3.

Замечание. Разумеется, нельзя слепо доверять графическим иллюстрациям. Может быть, нам только кажется, что точка А имеет координаты (1; - 1), а на самом деле они другие, например (0,98; - 1,01)?

Поэтому всегда полезно проверить себя. Так, в рассмотренном примере надо убедиться, что точка А(1; -1) принадлежит параболе у = - х 2 (это легко - достаточно подставить в формулу у = - х 2 координаты точки А; получим - 1 = - 1 2 - верное числовое равенство) и прямой у = 2х - 3 (и это легко - достаточно подставить в формулу у = 2х - 3 координаты точки А; получим - 1 =2-3 - верное числовое равенство). То же самое надо сделать и для точки 8. Эта проверка показывает, что в рассмотренном уравнении графические наблюдения привели к верному результату.

Пример 3. Решить систему

Решение. Преобразуем первое уравнение системы к виду у = - х 2 . Графиком этой функции является парабола, изображенная на рис. 18.

Преобразуем второе уравнение системы к виду у = 2х - 3. Графиком этой функции является прямая, изображенная на рис. 18.

Парабола и прямая пересекаются в точках А(1; -1) и В (- 3; - 9). Координаты этих точек и служат решениями заданной системы уравнений.

Ответ: (1; -1), (-3; -9).

Пример 4. Дана функция у - f (x), где

Требуется:

а) вычислить f(-4), f(-2), f(0), f(1,5), f(2), f(3);

б) построить график функции;

в) с помощью графика перечислить свойства функции.

а) Значение х = - 4 удовлетворяет условию -, следовательно, f(-4) надо вычислять по первой строке задания функции.Имеем f(x) = - 0,5x2, значит, f(-4) = -0,5. (-4) 2 = -8.

Аналогично находим:

f(-2) = -0,5. (-2) 2 =-2;
f(0) = -0,5. 0 2 = 0.

Значение удовлетворяет условию , поэтому надо вычислять по второй строке задания функции. Имеем f(х) = х + 1, значит, Значение х = 1,5 удовлетворяет условию 1 < х < 2, т. е. f(1,5) надо вычислять по третьей строке задания функции. Имеем f (х) = 2х 2 , значит, f(1,5) = 2-1,5 2 = 4,5.
Аналогично получим f(2)= 2. 2 2 =8.

Значение х = 3 не удовлетворяет ни одному из трех условий задания функции, а потому f(3) в данном случае вычислить нельзя, точка х = 3 не принадлежит области определения функции. Задание, состоящее в том, чтобы вычислить f(3), - некорректно.

б) Построение графика осуществим «по кусочкам». Сначала построим параболу у = -0,5x 2 и выделим ее часть на отрезке [-4, 0] (рис. 19). Затем построим прямую у = х + 1 и. выделим ее часть на полуинтервале (0, 1] (рис. 20). Далее построим параболу у = 2х 2 и выделим ее часть на полуинтервале(1, 2] (рис. 21).

Наконец, все три «кусочка» изобразим в одной системе координат; получим график функции у = f(x) (рис. 22).

в) Перечислим свойства функции или, как мы условились говорить, прочитаем график.

1. Область определения функции - отрезок [-4, 2].

2. у = 0 при х = 0; у > 0 при 0<х<2;у<0 при - 4 < х < 0.

3. Функция претерпевает разрыв при х = 0.

4. Функция возрастает на отрезке [-4, 2].

5. Функция ограничена и снизу и сверху.

6. y наим = -8 (достигается при х = -4); y наи6 . = 8 (достигается при х = 2).

Пример 5. Дана функция у = f(x) , где f(x) = Зх 2 . Найти.

Тема урока : Функция y =к x 2 , ее свойства и график .

Цель урока : обобщить и систематизировать знаний о квадратичной функции, ее свойствах и графике

Образовательные задачи:

закрепить основные свойства квадратичной функции y =kx 2 и ее график с применением компьютерного моделирования, интерактивной доски.

решение математических задач несколькими методами и способами, выявляя достоинства и недостатки каждого из них.

Развивающие задачи

развитие коммуникативных способностей учащихся,

развитие интеллектуально-исследовательской культуры учащихся,

развитие навыков компьютерного моделирования и работы на интерактивной доске

Воспитательные задачи:

воспитывать уважение к мнению других людей

серьёзное и ответственное отношение к учебному труду.

Вид урока: урок презентация, практикум.

Методы обучения: беседа, объяснение, деловая игра, демонстрация, компьютерное моделирование, практическая работа.

Формы организации работы с учащимися: индивидуальная, фронтальная, парная (групповая).

Оборудование: компьютер, мультимедийный проектор, интерактивная доска, обычная доска, миллиметровая бумага, раздаточный материал: разноуровневые задания, памятка с требованиями к выполнению практической работы.

Программное обеспечение: презентация, подготовленная в Microsoft PowerPoint ; Advanced Grapher 1.62 (Многофункциональная программа исследования математических функций с удобным графическим интерфейсом. Позволяет строить графики функций и их производных, находить экстремумы функций и корни уравнений, осуществлять интегрирование, получать таблицу значений функции по ее формуле и др., статус: freeware, авторские права: SerpikSoft, сайт: ); программное обеспечение интерактивной доски.

План урока.

1. Организационный момент – 1-2 мин.

2. Постановка целей и задач урока – 2 мин.

3. Оборудование – 1мин.

4. Повторение ранее изученного материала – 10 мин.

задания № 1

задания № 2

5. Практическая работа – 25 мин.

Задание № 3

Защита выполненного задания № 3

Задание № 4

Защита выполненного задания № 4

6. Домашнее задание – 2 мин.

7. Подведение итогов урока. Выставление оценок – 3 мин.

Ход урока

Демонстрируется слайд 1.

Этап I . Организационный момент.

Учитель приветствует ребят, отмечает отсутствующих, проверяет наличие чертежных инструментов, раздаточного материала: карточек-заданий, миллиметровой бумаги, памяток.

Постановка цели и задач урока

Демонстрируется слайд 2-5

Учитель. Сегодня мы подведем итог и проверим полученные знания и умения на практике, расширим и систематизируем знания о квадратичной функции y = kx 2 , как одной из математической модели. Продолжим освоение возможностей интерактивной доски, используя в работе компьютер, рассмотрим построении графиков квадратичной функций с его применением.

В реальной жизни встречаются процессы, описываемые различными математическими моделями вида y = f ( x ), г де f ( x ) - функция. В 7 классе мы познакомились с линейной функцией, в 8 классе начали знакомство с другой математической моделью, изучив f ( x ) – квадратичную функцию. Как вы научились отличать одну модель от другой, проверим в первом задании.

Этап II . Повторение.

Задание 1. Подпиши график функции.

Для каждого графика, изображенного на интерактивной доске, найти соответствующую ей функцию.

Демонстрируется слайд 6

На интерактивной доске учащиеся по цепочке, используя метод перемещения объектов (названия функций) из галереи рисунков, передвигают функции к соответствующему ей графику, при этом обосновывая свой выбор.

Остальные учащиеся в тетради и двое на обычной доске одновременно записывают функции в два столбика таблицы, указывая соответствующее значение k и b . Подводится итог работы. Ученики осуществляют взаимопроверку (на интерактивной и обычной доске, в тетрадях).

Классификация по виду математической модели

y = kx + b

y = kx 2

y = 3x + 2 ; k = 3 b = 2

y =3x 2 ; k = 3

y =2x ; k =2 b =0

y = - 3x 2 ; k =-3

y =2x ; k =2 b =0

y = x 2 ; k =1

прямая

парабола

Задание 2. Перечислить свойства квадратичной функции.

Демонстрируется слайд 7

Учитель. В математике важно отличать одну модель от другой, зная свойства каждой, уметь использовать различные языки (словесный, символический, графический) при описании этих свойств. При подготовке к уроку группа ребят систематизировала общие сведения о квадратичной функции в таблицу, используя символический язык. На интерактивной доске таблица свойств функций закрыта шторкой. Давайте вспомним, что нам известно о свойствах квадратичной функции.

После фронтально опроса по перечислению свойств квадратичной функции, используя прием шторки слева на направо, открывается первый столбик таблицы. Ребята сверяют по таблице, все ли свойства были названы. Затем перечисляются свойства функции в зависимости от коэффициента, в ходе беседы одновременно открываются строки таблицы – прием сдвига шторки вниз.

Заслушиваются ответы учащихся, подводится итог повторения свойств квадратичной функции. Учащиеся осуществляют самоконтроль.

Этап III . Применение знаний и умений

Практическая работа

Демонстрируется слайд 8

Задание № 3. «Построить и описать свойства кусочно-заданной функции

Учитель. Итак, теперь мы попробуем реализовать все знания на практике разными способами.

Сейчас вы разделитесь на три группы:

Группа № 1 «программисты » – строят график функции с помощью компьютера.

Группа № 2 «практики» – строят график функции без использования компьютера на миллиметровой бумаге.

Группа № 3 «теоретики» – описывают свойства данной функции.

Для ребят группы № 1 (посещающие факультатив по ИВТ), на интерактивной доске высвечивается алгоритм работы для компьютерного моделирования (Демонстрируется слайд 9), группа № 2 пользуется памяткой слайд 23, приложение № 2), группа № 3 имеет на столе уже готовый график данной функции, выполненный заранее учащимися на факультативе по ИВТ (слайд 14 ).

Задание для ребят группы № 2, со способностями ниже средних, разбито на подзадачи. Слабые учащиеся строят график только одной квадратичной функции, посильнее – квадратичную и линейную, продвинутые – выполняют все задание в комплексе.

Учитель проверяет задание у учащихся, выполнивших задание первыми в каждой группе. Далее по мере завершения практической работы учащиеся по цепочке проверяют задания друг у друга. Таким образом, у всех учащихся работы будут проверены. Те учащиеся, которые испытывают затруднения, обращаются за помощью к учителю либо к товарищам соседней пары.

Демонстрируется слайд 10-15

Защита выполненной работы

Каждая группа определяет лидера, ответственного для защиты работы. Учащиеся анализируют этапы построения и описания свойств функции. Учащиеся группы № 2 осуществляют самоконтроль, сопоставляя свой график с графиком на интерактивной доске, построенный с помощью компьютерного моделирования учащимися группы № 1. Учащиеся группы № 3 по цепочке комментируют свойства функции, график которой представлен на доске.

Во время защиты учитель задает вопросы, которые помогают выявить достоинства и недостатки каждого способа построения графика функции:

В чем преимущество данного способа построения графика функции?

Какие недостатки этого способа вы можете назвать?

Защита работы, выполненной с помощью компьютера

Демонстрируется слайд 16

Достоинства способа:

Наглядность, быстрота работы, точность построения, простота реализации, возможность автоматизации проверки результата; создается график не только на бумаге, но и в электронном виде.

Недостатки способа:

Не совершенствуются вычислительные навыки, отсутствует связь с теорией, наличие технических средств и программного обеспечения.

Демонстрируется слайд 17

Защита работы, выполненной без помощи компьютера

Достоинства способа:

Независимость от вычислительной техники при использовании; развитие вычислительных навыков, связь с теорией.

Недостатки способа:

Длительность работы по времени, нет точности в построении, невозможность автоматизации проверки результата; создается график только на бумаге.

Задание № 4 «Решить уравнение x 2 = 4 x - 4»

Демонстрируется слайд 18

Учитель. Предлагается вашему вниманию решить уравнение двумя методами: графический и аналитический

1. Графический метод – двумя способами (компьютерное моделирование и без помощи компьютера).

2. Метод – аналитический.

Анализируя этапы графического решения уравнения, учащиеся формулируют алгоритм выполнения задания. Демонстрируется слайд 19

При аналитическом методе решения необходимо вспомнить формулу квадрата разности двух выражений.

Графический метод решения можно представить двумя способами с помощью компьютерного моделирования и традиционно.

Задание выполняется учащимися групп № 1-3 по той же схеме, как и при выполнении практической работы задания № 3. Учащиеся выполняют задание и сверяют результат.

Защита выполненной работы.

Группа ребят, работающая у компьютера, демонстрируют результат работы с помощью мультимедийного проектора на интерактивной доске, указывая точку пересечения графиков функции и подписывая ее координаты. Группа учащихся № 3 – «теоретики», решение выносят на обычную доску. Группа учащихся № 3 – «практики», сверяют результат с интерактивной доской.

Демонстрируется слайд 20

Учитель дает задание сопоставить результаты. Определить на свой взгляд более эффективный метод.

Этап IV . Домашнее задание.

Демонстрируется слайд 21

Учитель. В классе вы работали в группах, в парах, выполняя вместе одно задание. Дома вам предстоит выполнить практическую работу с учетом ваших способностей. Задание дифференцировано по уровням сложности (слайд 22 -приложение 2, слайд 23 ). На доске демонстрируется слайд с предписанием выполнения работы.

Этап V . Подведение итогов урока. Выставление оценок.

Демонстрируется слайд 24

Сегодня мы обобщили и систематизировали знания по теме «Функция y =x 2 , ее свойства и график» с применением компьютерного моделирования, интерактивной доски, рассмотрели решение математической задачи несколькими способами, выяснили достоинства и недостатки каждого способа. Для вас более универсальным оказался способ – применение математического моделирования. Однако выбор конкретного способа зависит еще и от тех целей, которые мы ставим, решая ту или иную задачу. Разные математические задачи дают нам возможность применять различные приемы, методы и способы для конкретных практических задач. И вы вправе выбирать те из них, которые будут более подходящими в заданных условиях. На следующем уроке переходим к знакомству с новой математической моделью, пополняя запас изучаемых функций. Все знания и умения, полученные при построении графиков функций двумя способами, помогут вам в дальнейшей работе. Спасибо всем за работу.

Литература

Журнал «Математика в школе», № 10, 2008 г

Журнал «Информатика и образование», № 10, 2008 г.

А.Г.Мордкович. Алгебра 8 класс. Часть 1. Учебник. М.: Мнемозина, 2005 г.

А.Г.Мордкович. Алгебра 8 класс. Часть 2. Задачник. М.: Мнемозина, 2005 г.

Л.А.Александрова. Алгебра 8 класс. Самостоятельные работы / под ред. А.Г.Мордкович. М.: Мнемозина, 2006 г.

А.Г.Мордкович. Алгебра 7-9. Методическое пособие для учителя. М.: Мнемозина, 2000 г.

Приложение 1

Памятка

1. Как построить график функции.

Составить таблицу значений.

Построить точки на координатной плоскости.

Соединить точки плавной линией.

Подписать график функции.

2. Как найти значение функции f (x ) по графику.

На оси абсцисс найти соответствующее значение переменной.

Провести перпендикуляр на график функции, зафиксировать на нем точку.

Из данной точки провести перпендикуляр на ось ординат.

Точка пересечения с осью у – и есть значение функции f ( x ).

3. Как проверить принадлежность точки графику функции.

Найти значение функции от абсциссы точки.

Сопоставить результат с ординатой точки.

Если значения совпадают – точка принадлежит графику функции.

Приложение 2

Практическая работа

Вариант А

1. Построить график функции у = 2 х 2

а) значение у при х = -1; 2; 1/2

б) значение х , если у = -8

в) y наиб. и y наим. на отрезке [-1; 2]

3. Принадлежит ли графику функции точка А (-5; 50)?

Вариант В

1. Построить график функции у = - 0,5 х 2

2. Для данной функции найдите:

а) значение у при х = -2; 0; 3

б) значение х если у = - 8

в) y наиб. и y наим. на отрезке [- 4; 0]

3. Принадлежит ли графику функции точка А (-10; - 50)

Вариант С

1. Построить график функции у = 3/2 х 2

2. Для данной функции найдите:

а) значение у при х = 2; 1; 2/ 3

б) значение х если у = 6

в) y наиб. и y наим. на отрезке [- 2; 1]

3. Принадлежит ли графику функции точка А (-8;- 96)?

«Критические точки функции» - Критические точки. Среди критических точек есть точки экстремума. Необходимое условие экстремума. Ответ: 2. Определение. Но, если f" (х0) = 0, то необязательно, что точка х0 будет точкой экстремума. Точки экстремума (повторение). Критические точки функции Точки экстремумов.

«Координатная плоскость 6 класс» - Математика 6 класс. 1. Х. 1.Найдите и запишите координаты точек A,B, C,D: -6. Координатная плоскость. О. -3. 7. У.

«Функции и их графики» - Непрерывность. Наибольшее и наименьшее значение функции. Понятие обратной функции. Линейная. Логарифмическая. Монотонность. Если k > 0, то образованный угол острый, если k < 0, то угол тупой. В самой точке x = a функция может существовать, а может и не существовать. Х1, х2, х3 – нули функции у = f(x).

«Функции 9 класс» - Допустимые арифметические действия над функциями. [+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. В таких случаях говорят о графическом задании функции. Образование класса элементарных функций. Степенная функция у=х0,5. Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ.

«Урок Уравнение касательной» - 1. Уточнить понятие касательной к графику функции. Лейбниц рассматривал задачу о проведении касательной к произвольной кривой. АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у=f(x). Тема урока: Тест: найти производную функции. Уравнение касательной. Флюксия. 10 класс. Расшифруйте, как исаак ньютон назвал производную функцию.

«Построить график функции» - Дана функция y=3cosx. График функции y=m*sin x. Постройте график функции. Содержание: Дана функция: y=sin (x+?/2). Растяжение графика y=cosx по оси y. Чтобы продолжить нажмите на л. Кнопку мыши. Дана функция y=cosx+1. Смещения графика y=sinx по вертикали. Дана функция y=3sinx. Смещение графика y=cosx по горизонтали.

Всего в теме 25 презентаций

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.